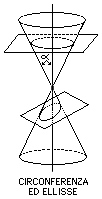
In geometria, le coniche sono tutte le curve generate dall'intersezione di un piano con la superficie di un cono circolare retto con le falde (ciascuna delle due parti opposte al vertice) infinitamente estese. Si consideri un cono, e sia a l'angolo compreso fra l'asse del cono e la sua generatrice. Se il piano secante forma con l'asse un angolo maggiore di a, l'intersezione che ne risulta è una curva chiusa detta ellisse; in particolare se il piano è perpendicolare all'asse, l'intersezione definisce una circonferenza, che si può considerare come una forma degenere di ellisse.

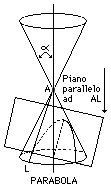
Nel caso in cui il piano formi con l'asse del cono un angolo esattamente uguale ad a, e quindi risulti parallelo alla superficie del cono, l'intersezione è una curva aperta infinitamente estesa, detta parabola.

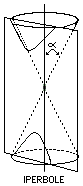
Infine, se il piano secante è inclinato rispetto all'asse del cono di un angolo minore di a, e non passa per il vertice del cono, la curva che ne risulta è un'iperbole. Entrambe le falde del cono vengono necessariamente intersecate dal piano, quindi l'iperbole è formata da due rami distinti, ciascuno dei quali infinitamente esteso.